Table of Contents
An Intro for Fellow History Buffs
Not Stopping Until You Have “The Best” Makes People Miserable
An Intro for Fellow History Buffs
First, a story: some kids spent Christmas break in 1955 playing with Radio Flyers or dolls. Katherine Frank helped develop artificial intelligence.
Over Christmas vacation, 1955, Herbert Simon tested the viability of the Logic Theory Machine by means of what can only be described as analog. Simon gave various family members cards to hold up—each of which represented a different subroutine—to test whether the cards could be held up in different orders, place themselves into various formations, to expedite the process of solving more complex problems.
In the early days of computer science and artificial intelligence, one notable problem in teaching machines how to solve multi-step problems—games and riddles that today would be considered simplistic—was that the number of options quickly spiraled out of control. A simple game could quickly grow beyond the processing capabilities in its attempt to compute each possible next step. While humans weren’t more accurate, they were more efficient, capable of intuitively inching towards a solution without the need for false starts and needless calculations.
Allen Newell and Herbert Simon, scientists who met while working at RAND, produced a program for proving theorems in symbolic logic. In discovering how to make their “Logic Theory” machine solve problems, Newell and Simon identified two necessary kinds of processes: subroutines (referred to as algorithms), and more complex processes (dubbed “heuristics”). Heuristics had three qualities:
- They were important, but not essential, to problem solving
- Their use depended on previous calculations and processes, as well as whatever information was available
- Their use was flexible enough to be used in different levels (problem-solving sets within problem-solving sets).
Heuristics were flexible ways of solving problems that maximized efficiency by using prior information. Got it. Over the next few years, Herbert Simon and Newell published papers outlining the actual heuristics used.
Our position is that the appropriate way to describe a piece of problem-solving behavior is in terms of a program: a specification of what the organism will do under varying environmental circumstances in terms of certain elementary information processes it is capable of performing… as we shall see, these programs describe both human and machine problem solving. We wish to emphasize that we are not using the computer as a crude analogy to human behavior.
Brains are Like Scissors
In 1953’s “A Behavioral Model of Rational Choice”—at the root of the field of judgment and decision-making—Simon clarified how he differentiated human thought from “perfect, utility-maximizing calculations”:
“Actual human rationality-striving can at best be an extremely crude and simplified approximation” to a perfectly rational cost-benefit analysis “because of the psychological limits of the organism (particularly with respect to computational and predictive ability.”
Unlike the infinite capacity of computer processing, human processing was limited by environmental and cognitive constraints, which he’d explain acted like a pair of scissors:

Behaviorism had been dominating the psychological landscape in the 1950s, and Simon’s “symbol processing approach” helped usher in the field of cognitive psychology. If you’ve been staring at monkeys to gain insight into human functioning, being told that you could now draw parallels between people and computers probably felt like the greatest gift in the world. So psychologists just went with it. This concept of bounded rationality has since confounded economists, wondering why humans often fail to maximize their outcomes in favor of reaching a “good enough” solution (also known as satisficing or settling).When we complain that cognitive biases and heuristics are inaccurate, it’s missing the point: our instinct is to optimize efficiency, given our psychological, mental, and biological constraints. Simon devised bounded rationality because he felt that computers had something to learn from our problem-solving instincts.
While the term heuristics may evoke a laundry list of possible errors in judgement and decision-making, it’s better thought of as a subset of strategies that allow us to reach functional answers with limited resources. One effect made famous by Nobel Prize-winning psychologist Daniel Kahneman is the anchoring bias, which occurs when a number that we’ve recently stumbled upon influences subsequent answers. For example, some visitors at the San Francisco Exploratorium were asked:
- Is the height of the tallest redwood more or less than 1,200 feet? What is your best guess about the height of the tallest redwood?
- Is the height of the tallest redwood more or less than 180 feet? What is your best guess about the height of the tallest redwood?
Group A estimated that the tallest redwood was 844′ tall. Group B—their ears still ringing from the idea of a 180′ tall tree—estimated the tallest redwood to be 282′ tall. The anchoring bias, Kahneman notes, is particularly helpful because, like video games, we can quantify it. People’s brains used the most accessible information—that irrelevant, initial number—and “increased the plausibility of a particular value” until reaching a satisfactory answer.1Ben R. Newell. “Judgment Under Uncertainty” in The Oxford Handbook of Cognitive Psychology, edited by Daniel Reisberg. (Oxford, UK: Oxford University Press, 2013.) In another study, Kahneman and Tversky had subjects spin a wheel that was “rigged” to land on either 10 or 65. After spinning the wheel and ending up on either 10 or 65, researchers asked the subjects two questions:
- “Is the percentage of African nations among UN members larger or smaller than the number you just wrote?”
- “What is your best guess of the percentage of African nations in the UN?”
If your wheel landed on “10,” you’d guess that 25% of the nations in Africa were in the UN, on average; if it landed on “65,” you’d guess 45%.
“Economists have a term for those who seek out the best options in life. They call them maximizers. And maximizers, in practically every study one can find, are far more miserable than people who are willing to make do (economists call these people satisficers).2“My suspicion,” says Schwartz, “is that all this choice creates maximizers.” Schwartz, author of The Paradox of Choice, was quoted in this excellent article in New York magazine.
Not Stopping Until You Have “The Best” Makes People Miserable
Economists say that satisficers—people who are fine with “good enough” answers, which frequently make use of shortcuts and heuristics—are irrational. But behavioral science and five minutes with that friend who insists on dragging everyone across state lines for “better dumplings” tells you that maximizers are the worst.
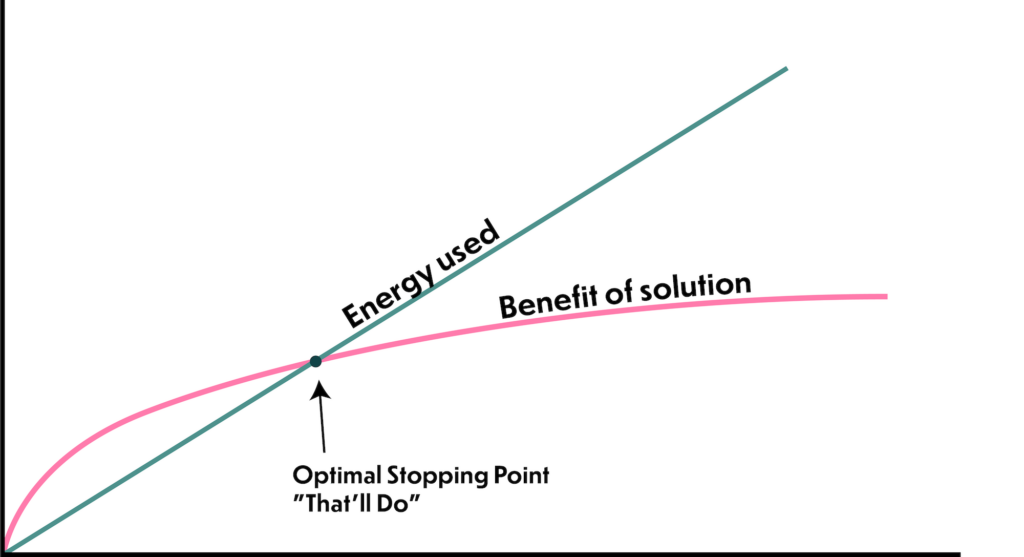
Both our time and energy are limited and precious—those are the things we hoard, rather than our need to be “right” when it comes to silly psychology studies, or lengthy calculations that don’t mean anything in the grand scheme of things.
The idea that humans are fundamentally irrational only makes sense if you’re assuming that humans have nothing better to do than work until they has the absolute perfect answer—and that the benefits of that answer are going to make up for the time and energy used to find it.
The “perfect” answer is one that uses as little energy as possible to arrive at a decent conclusion. Why would we keep working after we’ve found an answer that works? Your brain excels at one thing: achieving its goals while using as little energy as possible.
To save energy, our brain uses whatever information it has on hand to arrive at an answer. And why wouldn’t it use whatever is around? Pure mathematical randomness does not exist in nature; seeing berries in a bush or a snake on the ground usually implies the presence of other nearby food or foes. It’s so easy to create downfalls in these kinds of studies because of our tendency to see patterns—which, again, is completely logical from an evolutionary perspective. Evolution predisposed us to see patterns whenever possible; without making these kinds of inferences, we’d never be able to learn about our environment, decipher patterns, or develop a sense of causality in the world.3Andreas Wilke and Peter M. Todd, “The Evolved Foundations of Decision Making,” in Judgment and Decision Making as a Skill: Learning, Development, and Evolution, edited by Mandeep K. Dhami, Anne Schlottmann, and Michael R. Waldmann. (Cambridge, UK: Cambridge University Press, 2012): 3-27.
Our fundamental need for consistency and a sense of regularity may lead us to see patterns where none may exist, and use unrelated information to solve problems. But the “here’s a number/give me an unrelated answer” Kahneman/Yversky-style questions don’t exist in nature. Most answers in life are subjective. 99.99% of the time, it makes sense to use any information that we’d just heard for future thoughts; it doesn’t make sense to reevaluate every situation anew.
To recap: Randomness doesn’t really exist in nature—just in casinos and psychology experiments. To find the best answer using our time and energy well, we rely on energy-saving shortcuts, which work 99.9% of the time.
Humans do excel at finding the best answer, provided we consider the fact that the energy and time spent arriving at an answer count against its overall usefulness. For small decisions, there’s nothing wrong with intuitively maximizing what’s scarce to us: time.
- 1Ben R. Newell. “Judgment Under Uncertainty” in The Oxford Handbook of Cognitive Psychology, edited by Daniel Reisberg. (Oxford, UK: Oxford University Press, 2013.)
- 2“My suspicion,” says Schwartz, “is that all this choice creates maximizers.” Schwartz, author of The Paradox of Choice, was quoted in this excellent article in New York magazine.
- 3Andreas Wilke and Peter M. Todd, “The Evolved Foundations of Decision Making,” in Judgment and Decision Making as a Skill: Learning, Development, and Evolution, edited by Mandeep K. Dhami, Anne Schlottmann, and Michael R. Waldmann. (Cambridge, UK: Cambridge University Press, 2012): 3-27.